Toisella kerralla tutustuttiin pikaisesti eri kantalukujärjestelmiin:
Kymmenkantainen desimaalijärjestelmä (dec)
- symbolit: 0, 1, 2, 3, 4, 5, 6, 7, 8 ja 9
- merkintätapoja: 42, 42₁₀, 8’d42 (Verilog)
Kahdeksankantainen oktaalijärjestelmä (oct)
- symbolit: 0, 1, 2, 3, 4, 5, 6 ja 7
- merkintätapoja: 52, 52₈, 8’o52 (Verilog), 052 (C-sukuiset ohjelmointikielet, tätä kannattaa varoa!)
- vastaa kolmen bitin binäärilukua
16-kantainen heksadesimaalijärjestelmä (hex)
- symbolit: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E ja F
- merkintätapoja: 2A, 2A₁₆, 2ah, 8’h52 (Verilog), 0x2a (C-sukuiset ohjelmointikielet)
- vastaa neljän bitin binäärilukua (myös termiä nibble käytetään)
- kaksi heksanumeroa(digitaalia) vastaa kahdeksaa bittiä, eli tavua (myös termiä oktetti käytetään tietoliikenteessä)
Kaksikantainen binäärijärjestelmä (bin)
- symbolit: 0 ja 1
- merkintätapoja: 101010, 101010₂, 8’b0010_1010 (Verilog), 0b101010 (C-sukuiset ohjelmointikielet, ei standardi mutta monesti tuettu)
Lukujen esittäminen desimaalijärjestelmällä on ihmiselle se ymmärrettävin muoto. Mutta koska binäärisessä digitaalitekniikassa yksittäisillä signaaleilla on vain kaksi tilaa (HIGH/LOW, ON/OFF, 0/1, VCC/GND, jne.) ja näitä niputtamalla saadaan isompia lukuarvoja joita on monesti kätevämpi esittää binääri- ja heksaluvuilla. Nykyisin yleisin yksikkö on tavu (byte) joka koostuu kahdeksasta bitistä.
Tavulla voidaan ilmaista 256 (2×2×2×2×2×2×2×2 = 2^8) erilaista kombinaatiota. Nämä voidaan tulkita esimerkiksi lukuina 0..255 tai vaikka 7-bittisenä ASCII-merkkinä. Isompia lukuja voidaan rakentaa yhdistelemällä useampia tavuja, yleensä 2, 4 tai 8 kappaletta jolloin käyttöön saadaan 8-, 16-, 32- ja 64-bittiset luvut. Näistä huomataan, että ne ovat kaikki neljällä jaollisia, joten heksadesimaaleiksi niitä on helppo muuntaa.
Vastaavasti tietotekniikan alkuaikoina käytettiin paljon kolmella jaollisia bittimääriä (9, 12, 18, 24, 36 jne.) jolloin oktaaliluvut olivat luonnollisia.
Näissä kaikissa lukujärjestelmissä kokonaisluvut voidaan luetella saman kaavan mukaisesti, aloitetaan nollasta lisäämällä joka kierroksella lukuun yksi. Sitten kun tulos ylittää lukujärjestelmän symbolit, aloitetaan taas nollasta, mutta lisätään yksi tätä edelliseen symboliin.
- desimaalijärjestelmä:
- 0
- 0 + 1 = 1
- 1 + 1 = 2
- 2 + 1 = 3 …
- 8 + 1 = 9
- 9 + 1 = 10
- 10 + 1 = 11 jne.
- heksadesimaalijärjestelmä:
- 0
- 0 + 1 = 1 …
- 9 + 1 = A
- A + 1 = B …
- F + 1 = 10
- 10 + 1 = 11 (desimaalilukuna 17)
- binäärijärjestelmä:
- 0
- 0 + 1 = 1
- 1 + 1 = 10
- 10 + 1 = 11
- 11 + 1 = 100 (desimaalilukuna 4)
Huomioita
- nämä järjestelmät ovat vain saman informaation eri esitysmuotoja ihmisille, aina on kyse samasta matemaattisesta kokonaisluvusta, joka on olemassa esimerkiksi elektronisesti binäärilukuna johtimissa.
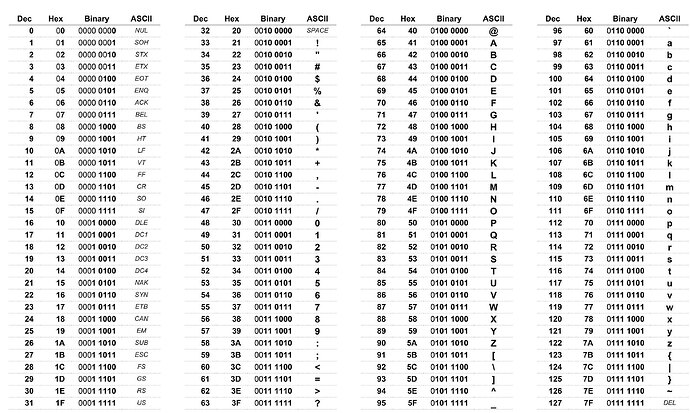
- binääriluvun voi pätkiä neljän bitin ryhmiin ja opetella vastaavat heksadigitaalit vaikka ulkoa (kuvan kuusitoista ensimmäistä riviä).
- binääriluvut/kombinaatiot voi helposti luetella ruutupaperille vaihtamalla alimman bitin arvoja nollasta ykköseen joka rivillä, seuraavan bitin arvoja kahden rivin välein, seuraavan neljän jne. tutki kuvasta bittien käyttäytymistä
- vaikka tässä puhutaan vain luvuista, ne voivat esittää ASCII-merkkejä, RGB-värejä, tietokoneohjelmaa jne.
Lukujärjestelmien välillä on jatkossa helppo tehdä muutoksia myös laskimella, perusteet voi testata vaikka sillä että ymmärtää mihin tämän vitsin ryhmään kuuluu: